Domain and Range
Videos: Finding the Domain of a Function (JMT)
Finding the Domain of a Radical Function (JMT)
Finding Domain and Range of Piecewise Functions (JMT)
Finding Domain and Range from a Graph (JMT)
More Finding Domain and Range from a Graph! (JMT)
Domain: The domain is the set of all possible x-values (inputs) in a relation. This means, that any number that can be used as x, is included in the domain. We usually write the domain as an interval of numbers like: x ≤ 0, or -2≤x≤2, or x can be all real numbers.
EXAMPLE 1: The domain of the relation {(2,1),(5,2),(1,5)} is 2, 5, & 1.
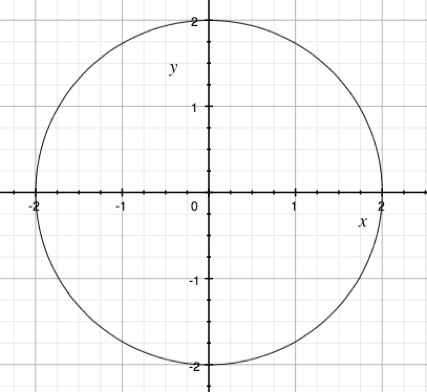
EXAMPLE 2: The domain of this relation is -2 ≤ x ≤ 2, because the first x-coordinate appears at -2, the last x-coordinate appears at 2, and there are points everywhere in between.
We can also get the domain of a function from it’s equation, which you might recall from your study in Algebra 2, of radical functions.
EXAMPLE 3: For √(x-2), the radicand (the stuff under the square root) has to be greater than zero, in order to show up on a normal graph. We can make an inequality to represent the domain, and solve for x:
EXAMPLE 4: For f(x)=x^4-3x^3+x^2, there aren’t any real numbers that you can’t plug into this function and not get a value. Therefore, the domain is: All Real Numbers
Range:
The range is the set of all possible y-values (outputs) in a relation. This means, that any number that can be used as y, is included in the range. We usually write the range as an interval of numbers like: y ≤ 0, or y can be all real numbers. For now, we can get the range by looking at a set of points, or looking at the graph of a relation and seeing where it exists in terms of y-values.