Functions and Relations
Relations are sets of ordered pairs. They look like this: {(2,1),(5,2),(1,5)}. Since ordered pairs represent points on a graph, we can also represent a relation as a graph, or as an equation.
Functions are a special kind of relation, where each x value (input), has a unique y-value (output). Using the same relation: {(2,1),(5,2),(1,5)}, we can see that if I input 2, I get 1 as an output. If I input 5, I get 2 as an output. If I input 1, I get 5 as an output. There’s no way to confuse them. This is a function.
Here’s a relation that isn’t a function. {(5,1),(5,2),(1,5)} If I input 1, I still get 5 as an output, but now if I input 5, I’m confused—I could get 1, or I could get 2 as an output. As soon as there are two potential y-values (outputs) for one x-value (input), our relation is not a function.
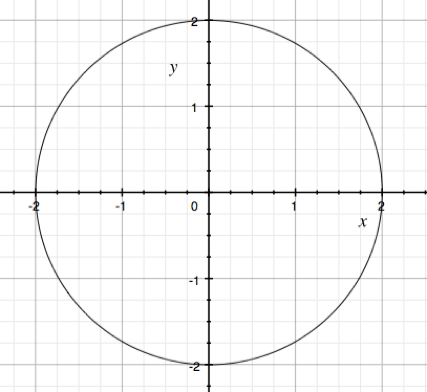
On a graph, we can use a shortcut called the vertical line test to see if a relation is a function. If there’s ever a time that we can draw a vertical line and it hits our graph in more than one place—it’s not a function. If vertical lines can only hit the graph once, it’s a function. Here are two graphs: the first one is a function, the second is not.
Function!
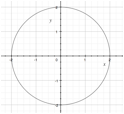
Not a function!